Adore__
[인공지능을 위한 선형대수] Linear Transformation 본문
Source : [BoostCourse 인공지능을 위한 선형대수 - 주재걸 교수님]
먼저 우리에게 익숙한 함수의 조건을 인지하고 시작하자

위와 같이 한 정의역이 동시에 두개의 y값을 갖는 것은 함수라고 할 수 없다.
▪️Linear Transformation 선형변환
Linear Transformation이란,
case 1) input들을 선형결합 -> 함수에 넣기 -> 나온 output
case 2) input을 먼저 함수에 넣음 -> output들로 동일한 선형결합을 수행
이 case 1 값과 case 2 값이 항상 같게 만드는 transformation을 선형 변환이라고 한다.

위 문제에서는 4x1 + 5x2 = 4T(x1) + 5T(x2)를 만족하므로 선형변환이라고 할 수 있다.
여기서 문제! y = 3x + 2라고 한다면 선형변환을 만족할까?

case 1) 3*(3*1+4*2)+2 = 35
case 2) 3(3*1+2) + 4(3*2+2) = 47
둘의 값이 다르므로 선형 변환이라고 할 수 없다.
이처럼 함수에 bias (여기서는 2)이 포함되면 선형결합이라고 하지 않는다.
하지만 그럼에도 불구하고 선형변환을 만족하도록 바꿀 수 있는 방법이 있다. 즉, 위 상황을 bias가 없는 선형결합의 식으로 만들 수 있다.
어떻게? 우선 위 문제는 1차원에서 1차원으로 가는 선형변환이었다. (R1 -> R1)
하지만 y 식을 벡터로 바꿔서 표현하면, 2차원에서 1차원의 변환이 된다. (R2 -> R1)
이전 상황에서 x=1이 이었던 것이 [1,1]이 되고, x=2는 [2,1]이 되면서 상수 term이 사라지므로 선형변환이 가능하다.
[1,1]과 [2,1]을 사용하여 case 1)과 case 2)를 동일하게 수행해보면, 동일하게 47이 나온다.

이처럼 벡터들의 차원을 바꿔서 선형변환을 만족시킬 수 있다.
▪️Matrix of Linear Transformation

이 문제에서 우리는 'T는 선형성을 만족하는 변환이다'라는 조건과 T([1 0]), T([0 1]) 2가지의 정보를 갖고 T를 해석할 수 있다.
이전에 다루었던 standard basis vector를 떠올려보자.
이를 이용하면 [x1 x2]를 x1*[1 0] + x2*[0 1]로 바꿔 표현할 수있다.
이후 선형변환 성질을 이용하여 standard basis vector에 먼저 함수를 처리하여 2가지 조건을 사용할 수 있다.
이후 column의 combination으로 coefficient와 matrix를 하나로 모으면, 더 간단하게 표현이 가능하다.
정리하자면, 선형성을 만족하는 변환이다? => 무조건 Matrix와 주어진 입력벡터의 곱으로 나타낼 수 있다.
이를 일반화를 시켜보자.


모든 선형변환은 matrix A와 입력벡터 x의 곱으로 표현 (T(x) = Ax)이 가능하고,
이때 A는 선형변환 T에 해당 차원의 standard basis vector를 하나씩 집어 넣어서 나열한 것이다.
오른쪽 예시를 보면 이해를 도울 수 있다.
▪️Linear Transformation in Neural Networks
그렇다면 이러한 선형변환이 Neural Networks에서 왜 중요할까?
우선 아래 영상은 선형변환을 통해서 이루어지는 layer를 시각화 한 것이다.
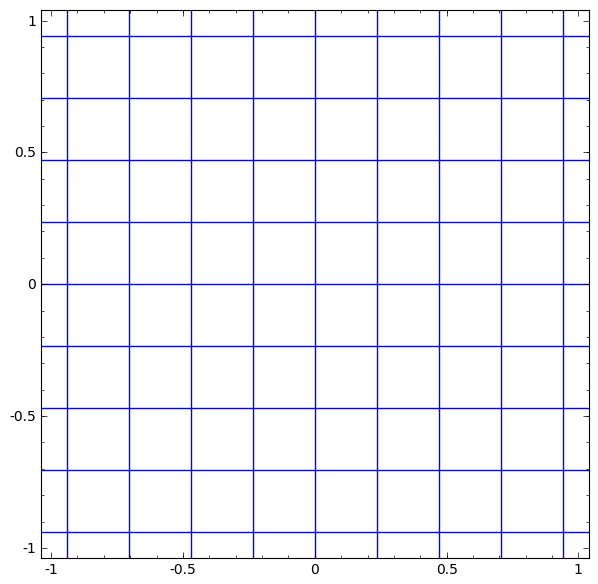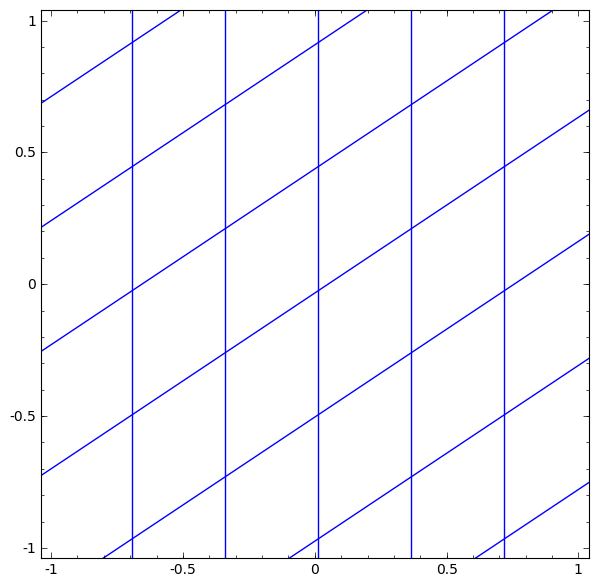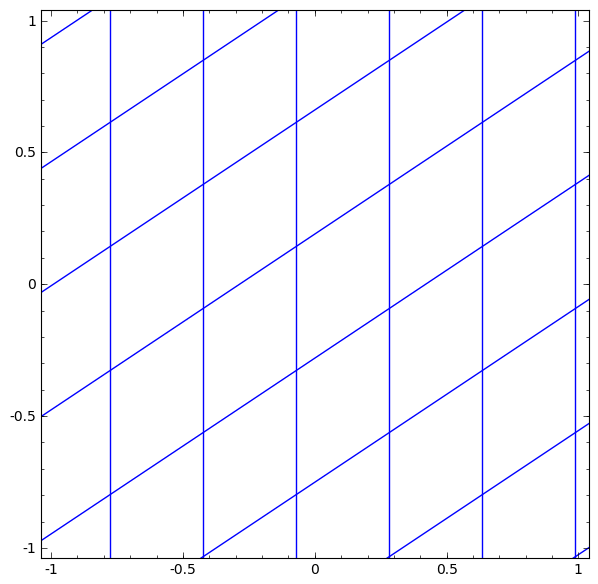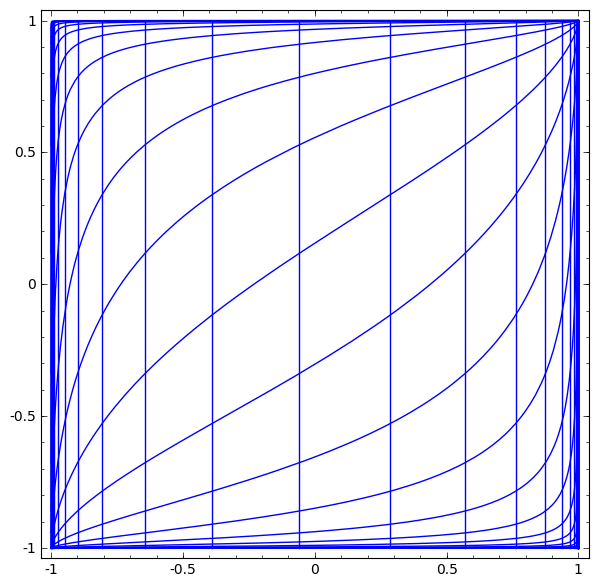
2차원에서 2차원으로 변환하는 layer가 있다고 하자.
여기서 선형변환의 의미하는 것이 무엇일까?
좌표값의 왜곡을 통해서 작은 정사각형을 기울어진 평행사변형과 같은 꼴로 바꿔주는 것이다.
(영상을 보면 정사각형이 평행사변형으로 바뀜. 그리고 위치가 움직이는 것은 bias에 의한 것으로 생각하면 됨)
이러한 변환은 convolution layer나 fully connected layer에서 사용되는 기본적인 방법이다.


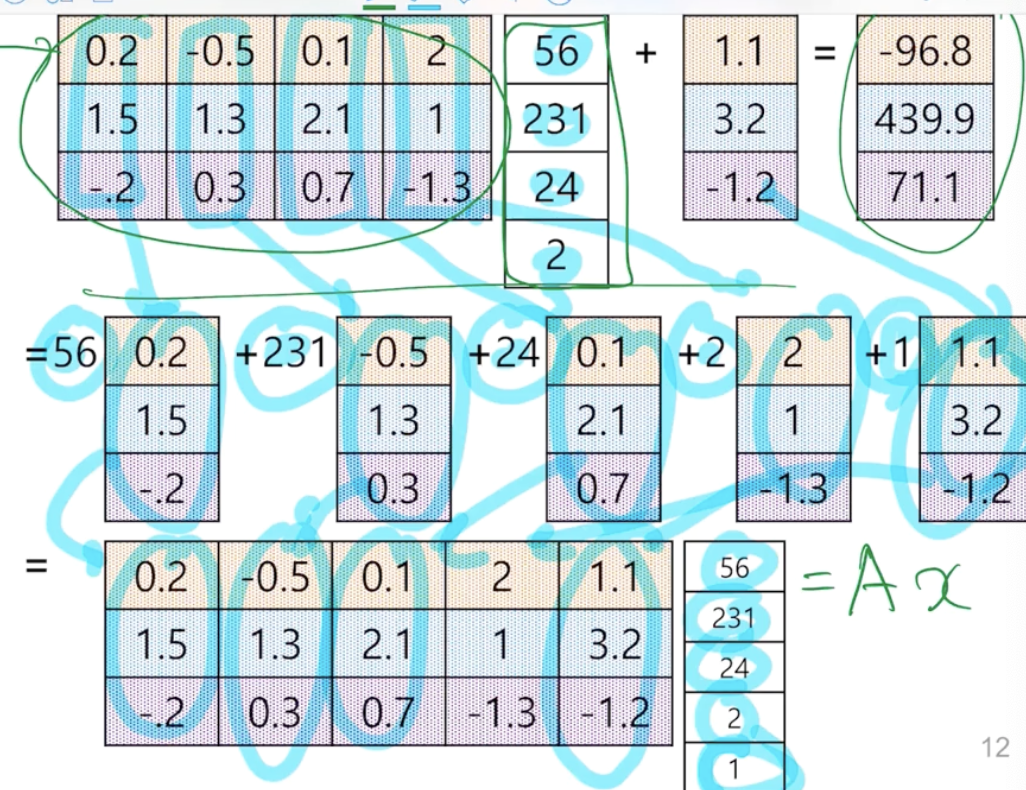
input을 키, 몸무게, 혈당, 나이로 각각 집어넣어서 당뇨/고혈압/폐암일 확률을 구한다고 가정해보자.
4개의 node 하나하나마다 score가 들어가면(행렬 A) input값으로 넣어주었던 상수배(56, 231, 24, 2,1)만큼을 output에 전파해주는 방식이다.
bias term이 항상 존재하는 경우에도 앞서 보았던 방법으로 해결할 수 있다.
coefficient는 1로 설정해서 bias와 곱한 term을 뒤에 추가로 더해준 후 column combination으로 하나로 모으면 된다.
교수님께서 추천하시는 blog
Home - colah's blog
colah.github.io
'Basis > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 2.1 Least Squares (1) | 2023.04.28 |
|---|---|
| Singular Value Decomposition (SVD) (0) | 2023.04.27 |
| [인공지능을 위한 선형대수] Onto / One-to-one func (0) | 2023.04.19 |
| [인공지능을 위한 선형대수] Subspace, Basis, Dimension, Rank (0) | 2023.04.18 |
| [인공지능을 위한 선형대수] Linear Independency (1) | 2023.04.18 |




