Adore__
[인공지능을 위한 선형대수] 2.1 Least Squares 본문
Source : [BoostCourse '인공지능을 위한 선형대수' - 주재걸 교수님]
방정식의 개수(열벡터)가 변수보다 클 때, 보통 '해가 없다'라고 말한다.
방정식의 개수가 많아지면 하나의 열벡터는 엄청 광활한 dimension 안에 있다는 것이다.
여기서 해가 존재한다는 것은 이보다 적은 벡터의 span 공간 안에 b벡터가 들어가야한다는 것인데,
광활한 (예를 들어 100 dimension) 전체 공간에서 아주 작은 3개 벡터의 span 공간 안에 b 벡터가 딱 들어갈 확률은 그으윽히 작다.

이러한 경우 해는 어떻게 구해야할까?
단순히 해가 없네~라고 끝낼 수 없다. 근사적으로라도 해를 구해보자! 라는 게 Least Squares가 등장한 배경이다.
먼저 기본적인 내용을 살펴보자
Basis
▪️Inner Product (내적)
같은 공간에 있는 두개의 벡터가 있을 때, 두 벡터의 내적은 행렬의 곱이다.

내적의 연산은 선형변환이라고 할 수 있다.
(2개의 벡터를 먼저 내적하고 선형결합을 하는 것 )= (먼저 선형 결합 후 내적을 하는 것) 이 두개가 같기때문이다.

▪️Vector Norm
Vector의 길이를 norm이라고 부른다.

여기서 중요한 점은 자신의 길이가 자기 자신의 내적으로 정의될 수 있다는 것이다.
▪️Unit Vector
방향은 바뀌지 않고, 길이만 1로 바뀐 것을 단위벡터라고 한다.

이후에도 두 벡터간의 각도, 직교벡터, 등 내용이 있는데 이미 대학수업에서 많이 다룬 내용이라 넘어가겠다
Least Squares
다시 처음 봤던 그 문제로 돌아와보자
주어진 방정식이 4개, 변수가 3개일때 앞서 말한것처럼 정확한 해를 구할 순 없다. 하지만 우리는 해에 근사 하는 값은 찾을 수 있다.
먼저 방정식 4개중에서 3개로만 구한 해 x1,x2,x3를 구한다. 그리고 이를 Ax 에 대입해서 b^을 얻어내자.
우리는 마지막 방정식을 고려하지 않았기때문에 b^은 b와 완전히 같을 수 없고 어느 정도 차이가 생기게 된다. ( |b-Ax| )
이 차이값을 최소로 하는 x를 구하는 게 우리의 목표이다! (최대한 원래의 b와 근사한 b^을 만들 수 있는 x를 찾자!)
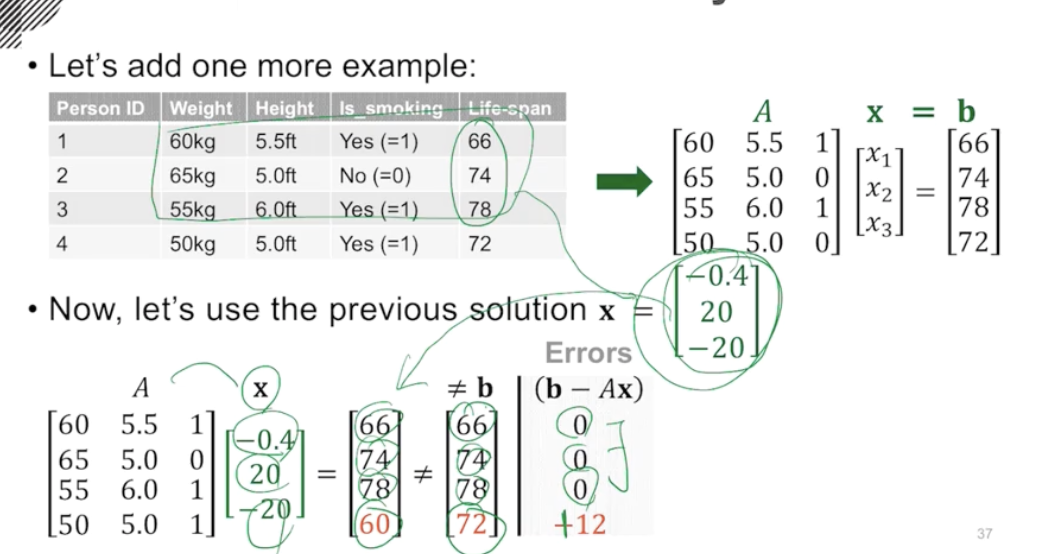

위 그림에서 주어진 후보 x가 2개 있을 때, 둘 중에 어떤 것이 원래 b와 근사한 b^를 얻어낼 수 있는지 확인해야 한다.

즉, |b-Ax| 값이 최소로 하는 x를 선택하면 두번째 x값이 된다.
신기하게도 3명 다 맞추고 마지막 4번만 오차가 심한 것보다, 고루고루 적은 오차를 보이는 x값이 더 최적의 해가 된다.
이를 일반화 하면 다음과 같은 식으로 근사해 x^를 표현할 수 있다.

min |b-Ax| 는 오차의 최소값을 구하는 식이고, 이때 arg를 사용하는 이유는 이 최소값을 만드는 x를 불러오기 위한 함수이다.
✔︎ 어떤 solution vector x를 썼을 때, coefficient vector A와 곱해서 나온 결과벡터와
실제 b벡터의 차이 (error)를 최소로 하는 x 벡터를 구하기
기하학적으로 Least Square 살펴보기
앞선 예시에서 봤던 Ax를 다음 그림과 같이 표현하면 3개의 열벡터의 선형결합으로 표현할 수 있다.
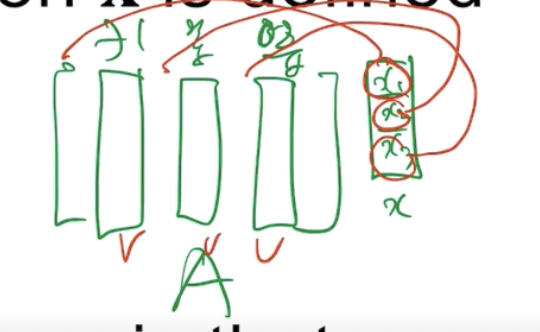
따라서 x값을 아무리 바꿔도 Ax는 A의 열공간에 포함되어야 한다는 제약이 있다.
이를 Least Square 문제 관점으로 바라보면,
우리는 A의 열공간에 있을 수 밖에 없는 어떤 벡터 중에 주어진 b 벡터와 가장 가까운 벡터를 찾고, 이때의 x벡터를 구하는 것이다.
이해하기 쉽게 다음 그림을 보자.
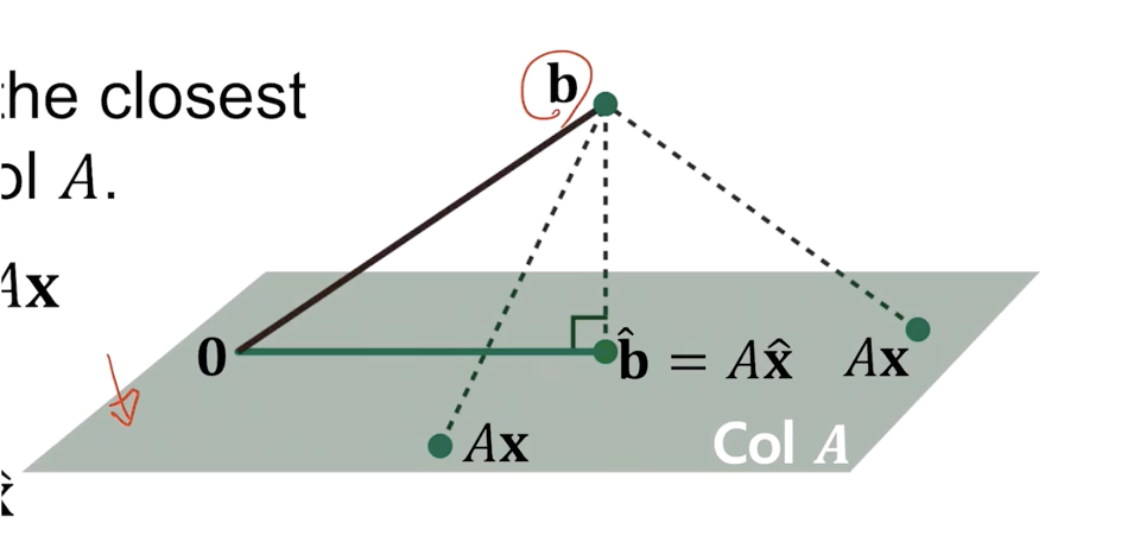
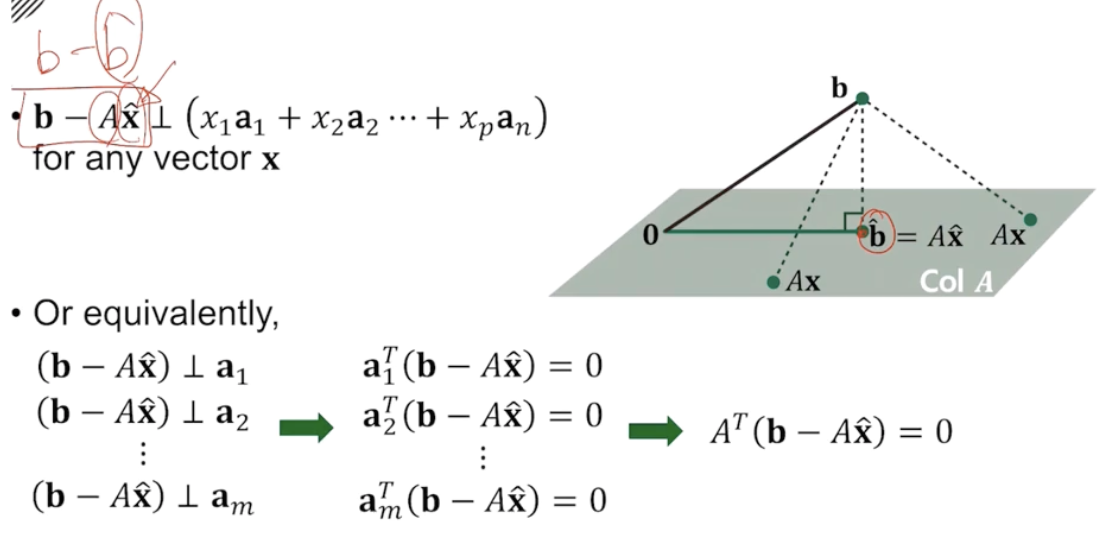
A의 열공간을 초록색 평면으로 두고, 우리에게 주어진 b 벡터는 이 열공간 밖에 있다. 따라서 원래는 해를 구할 수 없다.
하지만 우리는 b와 가장 가까운 점(b^)을 초록색 평면에서 찾고, 이를 만드는 x^를 찾아야한다.
그렇다면 b와 b^이 가장 가깝다는 것 무엇일까?
고등과정에서 배웠지만, 점 b에서 평면에 수선을 내렸을때 만나는 점이 가장 짧은 거리의 b^이 된다.
즉,(b-b^ 벡터 ㅗ Ax) 를 만족하는 x!
이 식을 풀어서 써보자. 먼저 Ax = x1*a1 + x2*a2 + x3*a3 (이때 x1,x2,x3는 상수, a1,a2,a3 은 열벡터)와 같다.
어후 말로 설명하기 힘드니 손으로 적어보자...
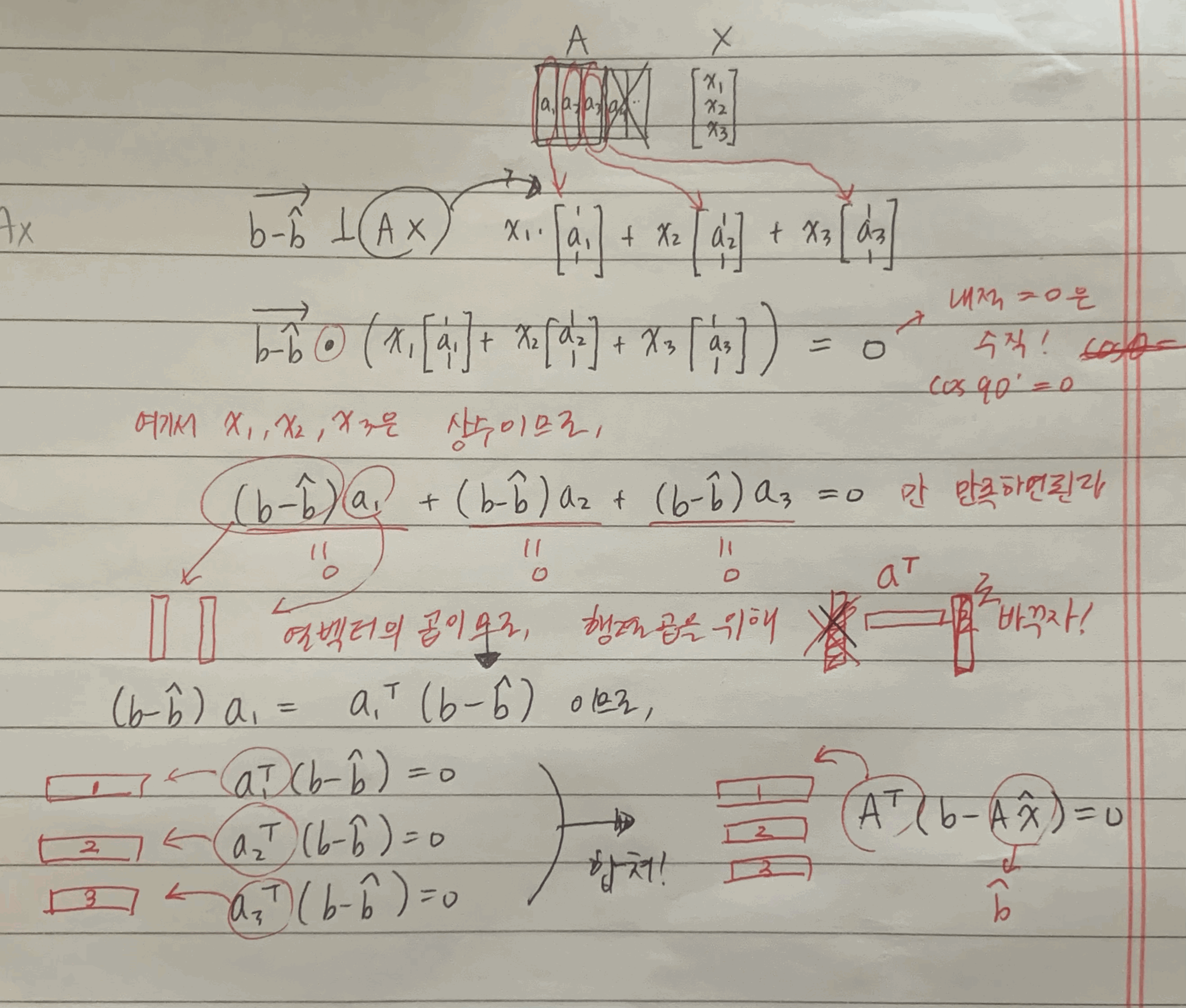
위 필기로 대략 이해하고 아래 교수님의 자료를 보면 좀 이해가 편하지 않을까..싶다!
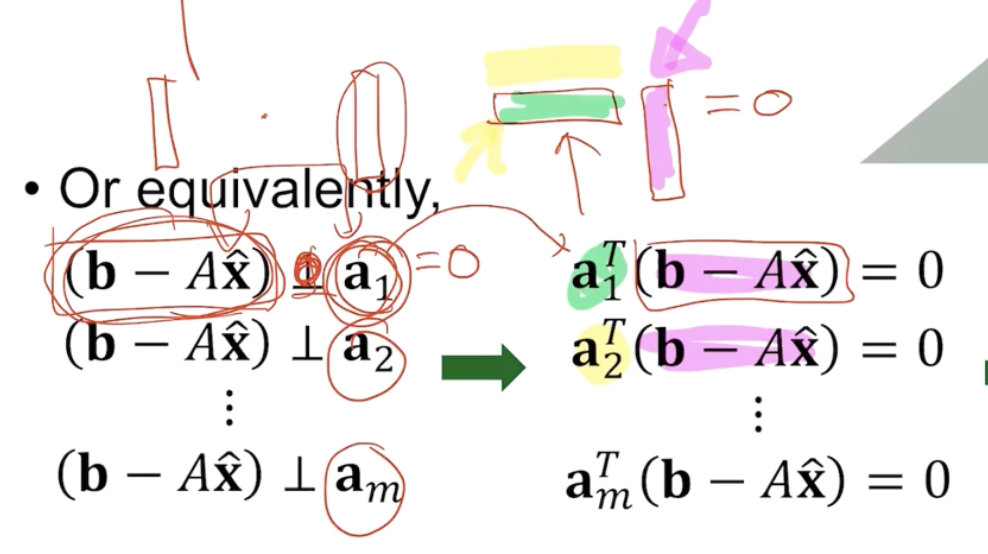
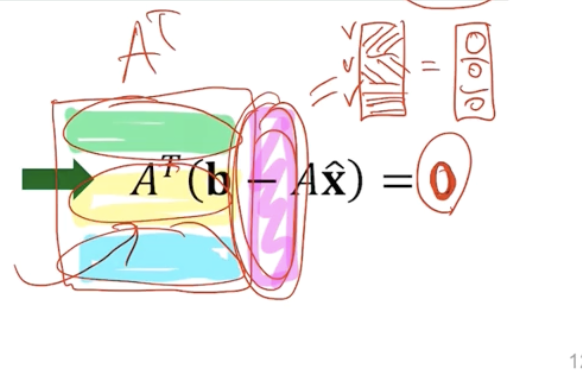
이때 최종적으로 나온 저 식이 정규방정식이다.
다음 포스팅에서는 'Normal Equation'에 대해 알아보자
'Basis > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수학] 3.5 Eigendecomposition (0) | 2023.04.30 |
|---|---|
| [인공지능을 위한 선형대수] 2.2 Normal Equation (0) | 2023.04.28 |
| Singular Value Decomposition (SVD) (0) | 2023.04.27 |
| [인공지능을 위한 선형대수] Onto / One-to-one func (0) | 2023.04.19 |
| [인공지능을 위한 선형대수] Linear Transformation (0) | 2023.04.19 |




