Adore__
[인공지능을 위한 선형대수학] 3.5 Eigendecomposition 본문
만약 행렬 A가 대각화가 가능하다면 (diagonalizable), 다음과 같은 식이 성립할 것이다.

여기서 D는 대각행렬, V는 가역행렬이어야 한다.
이 식을 살짝 바꿔서 A를 기준으로 만들어보자

이 꼴을 바로 A의 eigendecomposition이라고 한다.
주어진 A를 여러 개의 matrix 곱으로 나타내되, 이를 고유값 분해로 부르기위해서는 V와 D가 어떤 조건을 만족해야 한다.
V는 가역행렬이고, D는 대각행렬이어야 한다. 음? 앞의 대각행렬의 조건과 같다.
따라서 A가 대각화가 가능하다면, 고유값분해가 가능하다는 것과 동치이다.
자 그러면 A가 고유값 분해가 가능하다고 가정하고, x의 선형변환을 A matrix로 설정해보자.

A의 고유값 분해 식에 의해 Ax를 다음과 같이 바꿀 수 있다.

이 식의 의미를 생각해보자.
고유값을 구하는 목적은 복잡한 행렬곱 대신 상수인 고유값만 곱하여도 값이 같으므로, 계산을 간소화하는 것이었다.

하지만 입력벡터가 고유벡터가 아니라면? 위 그림처럼 고유값으로 간단하게 표현할 수 없다.
eigen decomposition 를 통해서 어떤 벡터가 주어져도 고유값의 선형결합 '처럼' 나타낼 수 있도록 하는 것이다.

위 그림처럼 어떤 벡터 x가 주어져도 (혹시 고유벡터가 아니더라도), 이들을 고유벡터들의 선형결합으로 표현하고
이들의 고유값과 각각 곱하여 효율적인 식으로 변환한 후에, 나중에 합치겠다는 것이 고유값분해의 목적이다.
이를 어떻게 하느냐?
단계단계 보자~
1) Change of Basis
2차원 공간에 basis는 여러가지 경우가 있다.
(basis는 유일하지 않다. 다만 기저벡터의 개수와 기저벡터로 어떤 한 벡터를 표현하는 선형결합계수는 유일)
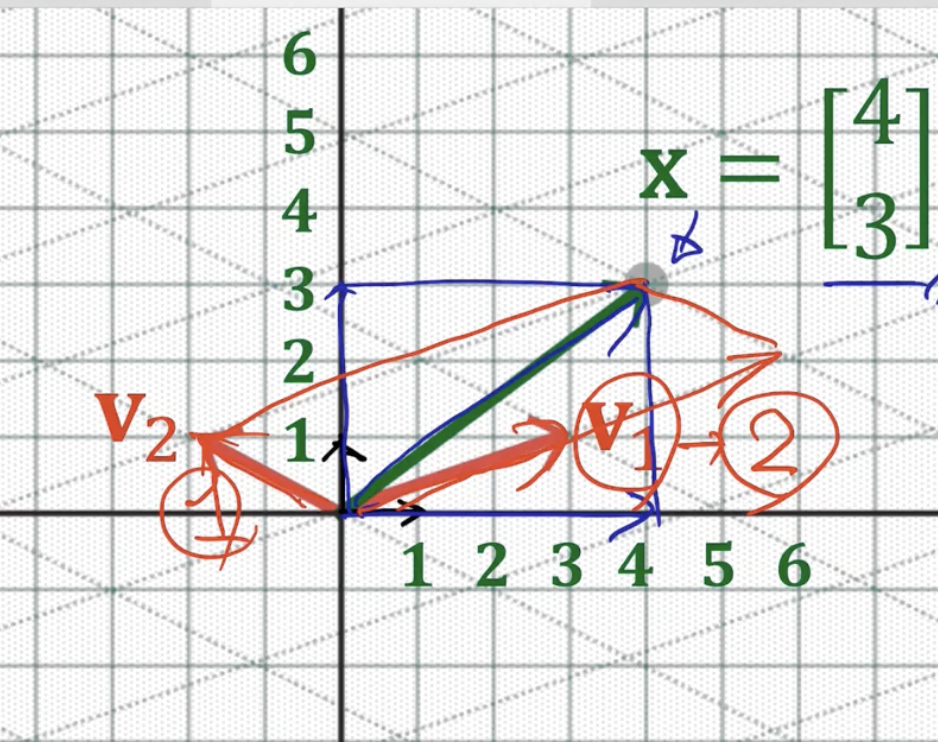
위 그림에서 x = [4 3] 이 주어졌을 때, 기저는 다양하게 있을 수 있다.
가장 기본적인 기저는 { [0 1], [1 0] }으로, 이들의 선형결합(가로는 4배, 세로는 3배) 으로 x 점까지 평행사변형 (파란색)을 만들 수 있다.
이번엔 다른 기저 {v1, v2}를 사용해서 점 x까지 평행사변형을 만들어보자.
v1 = [1 3] , v2 = [-2 1]이라 할 때, v1는 2배 길이를 늘려야하고 v2는 1배만큼 늘리면 된다.
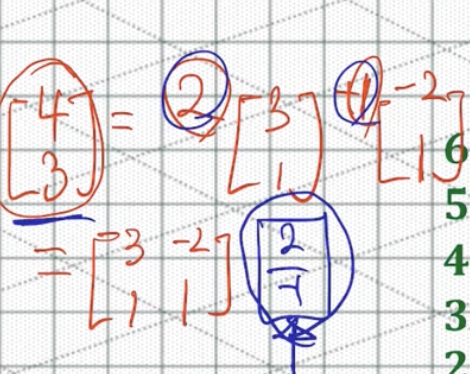
따라서 v1와 v2에 각각 곱한 [2 1] , 또는 길이를 늘린 비율이 선형변환의 계수가 된다.
만약 v1와 v2가 기저임과 동시에 고유벡터라면, 이전에 보여줬던 것과 같이 고유값의 곱으로 Ax 선형변환을 간단하게 바꿀 수 있다.

정리하자면, '기저변환'의 목적은
어떠한 벡터 x가 주어졌을 때, 이를 고유벡터들의 선형결합으로 표현하기 위해 이들을 기저로 삼는다.
그러면 기존 기저와 다른 선형 결합으로 표현해야 하고, 이때 적합한 선형결합계수 (위 그림에서는 [x1 x2])를 찾아야 한다.
만약 고유벡터(동시에 기저벡터)의 행렬 V가 가역행렬이라면, V inverse * x로 이 계수를 구할 수 있다.
✔︎ Ax = VDV(inverse)x의 첫번째 변환
2) Element-wise Scaling
대각행렬의 곱은 매우 간단하다는 장점이 있다.
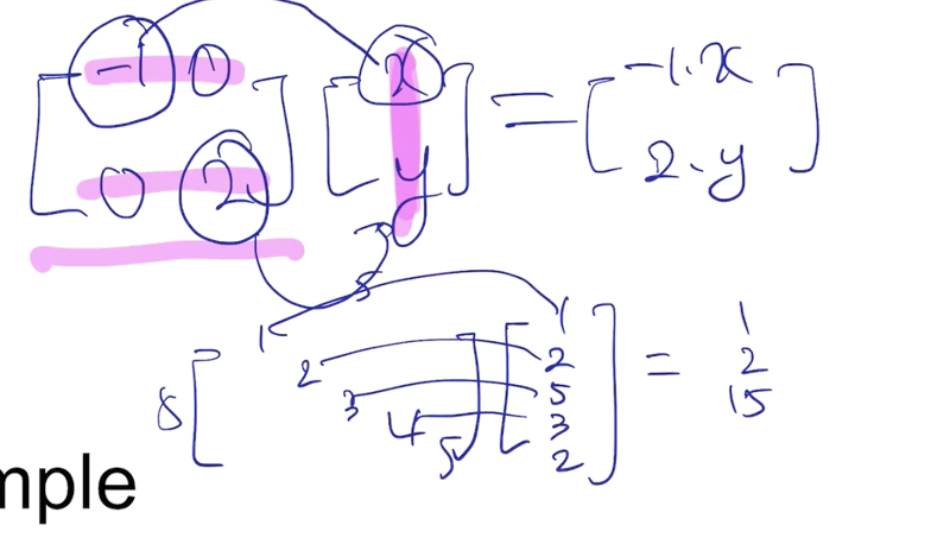
커다란 행렬의 곱으로 보일 수 있지만, 사실상 elements 끼리의 간단한 곱셈이다. (계산상의 이점)

y를 '기저변환'에서 x를 표현하기 위해 고유벡터에 각각 곱했던 계수으로 생각하면, 다음 합성함수로 넘어갈 때 Dy가 된다.
이때 D는 A에 대한 고유값들의 대각행렬로, D의 element에 이 계수(y)만 각각 곱하면 된다.
3) Back to Original basis
현재 Dy의 결과값 z는 아직까지 앞서 바꿨던 x의 고유벡터이자 기저벡터 v1, v2를 기준으로 설정된 좌표이다.
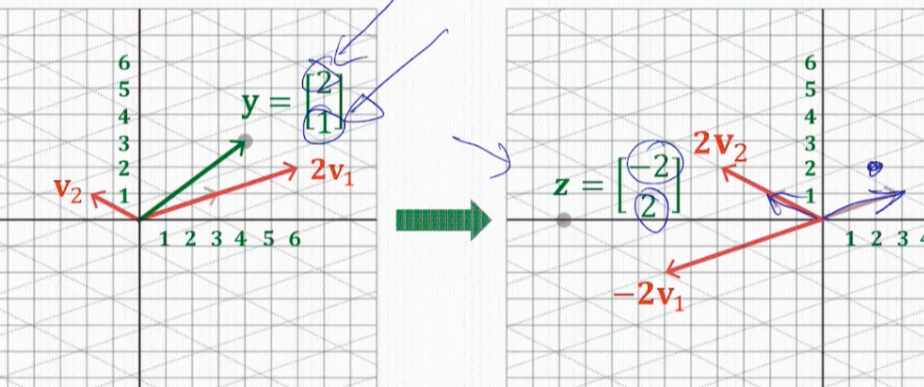
따라서 이를 다시 원래 기존 기저로 바꿔주는 작업이 필요하다.

🔻정리
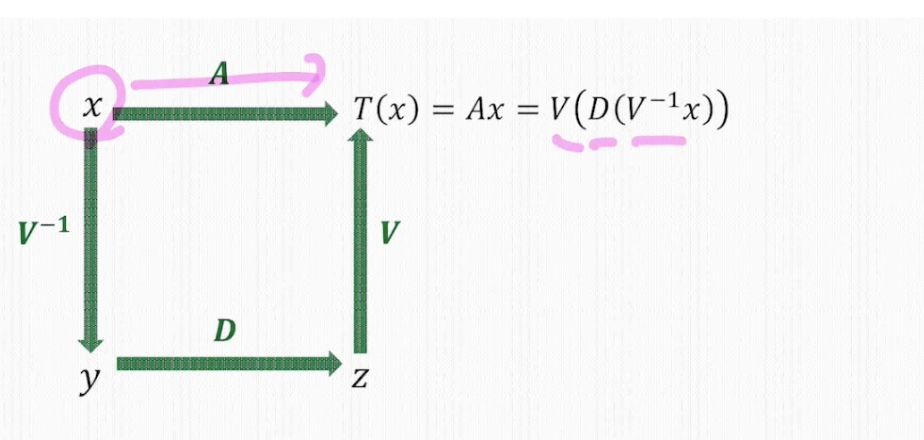
V-1 : x를 새로운 좌표계로 바꾸기. 즉, 고유벡터를 기저로 하여 새로운 좌표계 구하기 (새로운 기저를 얼마만큼 늘려야 x를 표현하는지)
D : Ax 대신 간단하게 고유값 곱하기
V : 원래 좌표계로 복원하기
만약 선형변환 A를 한번만 하는 게 아니라 k번 한다면?

기저를 바꿔서 다른 좌표로 갔을 때, 거기서 고유값 D를 곱해서 선형변환 한것을 k번하고 다시 기존 좌표계로 돌아온다.
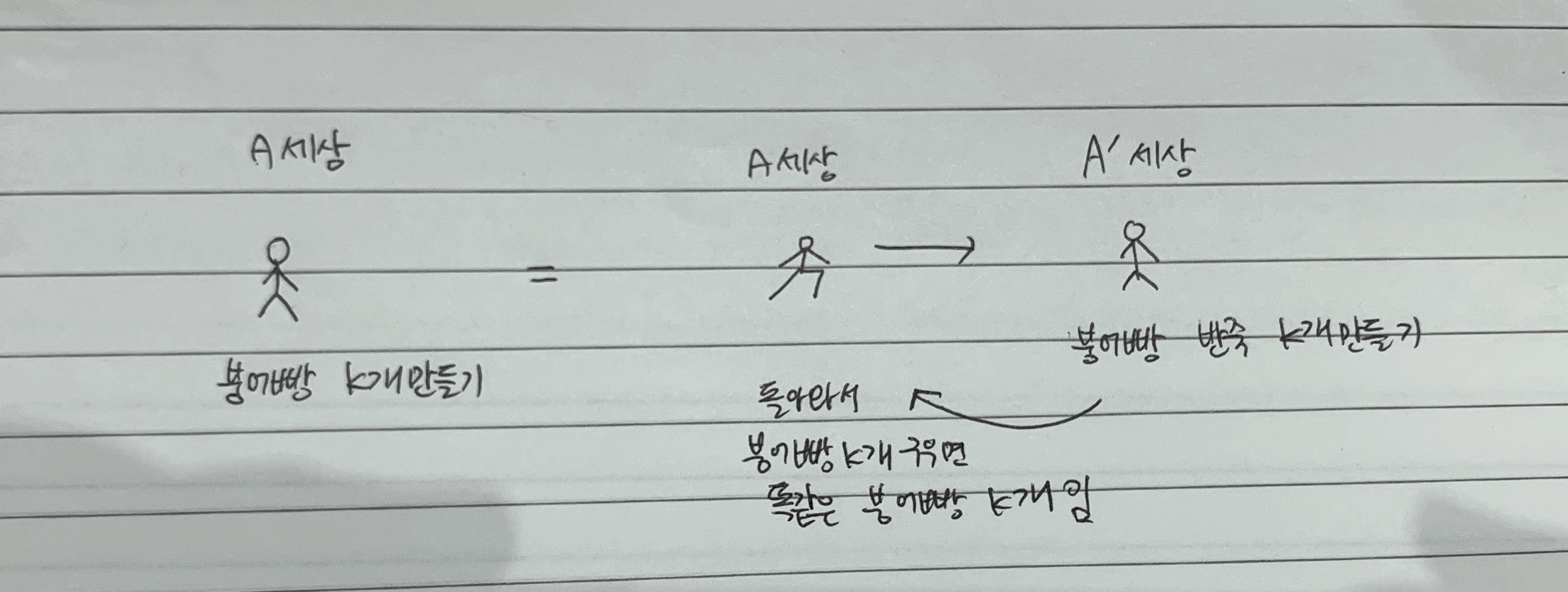
이해하기 쉽게 표현하면, 내가 살고 있는 세상에서 어떤 일을 k번 한다고 할 때, 평행우주로 다른 차원에서 이 일과 동일하게 할 수 있는 작업을 k번 한 후에 다시 내 세상으로 돌아오면 같은 작업이 된다는 것이다.
'Basis > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 4.2 고유값 분해와 특이값 분해 응용 (0) | 2023.05.01 |
|---|---|
| [인공지능을 위한 선형대수] 4. Singular Value Decomposition (1) | 2023.05.01 |
| [인공지능을 위한 선형대수] 2.2 Normal Equation (0) | 2023.04.28 |
| [인공지능을 위한 선형대수] 2.1 Least Squares (1) | 2023.04.28 |
| Singular Value Decomposition (SVD) (0) | 2023.04.27 |




