Adore__
[인공지능을 위한 선형대수] 2.2 Normal Equation 본문
Source : [BoostCourse '인공지능을 위한 선형대수' - 주재걸 교수님]
정규방정식, 즉 근사해를 구하는 방법은 크게 2가지로 나뉠 수 있다.
1. (A transpose * A)가 가역행렬일 경우
앞서 Least square에서 x^를 찾기 위해 출발했던 식은 아래 그램의 x^이었다.
이 x^를 minimize 하는 식을 구하면 결국에 Normal Equation 인 A transpose *(b-Ax) = 0와 같다.



따라서 A가 가역행렬일 경우, 위의 마지막 식처럼 근사해 x를 구할 수 있다.
2. (A transpose * A)가 가역행렬이 아닐 경우
역행렬이 없다는 것은 해가 무수히 많거나, 없는 경우 두 가지 중 하나이다.
하지만 보통 정규 방정식에서는 '해가 없는 경우'는 존재하지 않는다. 따라서 역행렬이 없을 때는 해가 무수히 많은 경우이다.

언제 역행렬이 존재하지 않는가?
A의 열벡터들이 선형 독립이면 역행렬이 존재하지만, 선형 종속이면 A transpose * A의 역행렬이 존재하지 않는다.

위 그림에서 평면의 수선의 발인 b^은 한 점밖에 없을 것이다.
x^는 원점에서 점 b^까지 잇는 평행사변형을 만드는 A 벡터들의 길이를 조절하는 상관계수이다.
이 x^가 하나밖에 없을 때는 A 열벡터가 선형 독립이고 (한가지 방법으로만 평행사변형 만들 수 있음)
x^가 여러가지 존재할 때는 A 열벡터가 선형 종속이다 (다양한 방법으로 평행사변형 만들 수 있음) == AtA가 역행렬이 존재하지 않는다.
하지만! A(t)*A가 가역행렬인 아닌 경우(A의 열벡터가 선형 종속인 경우)는 극히 드물다.
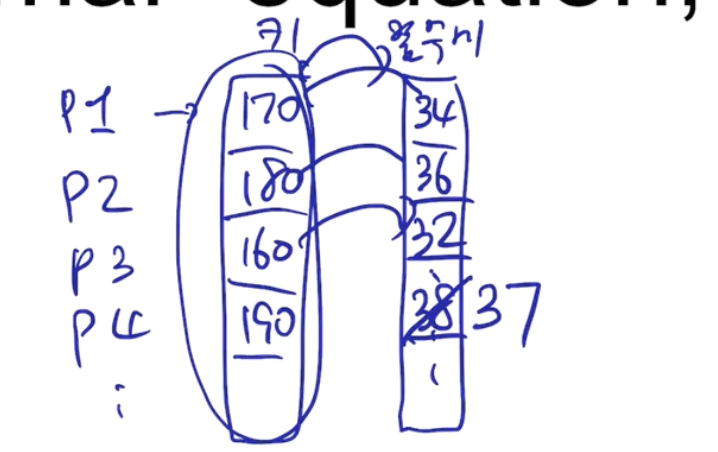
사람들의 키와 몸무게를 조사한다고 할 때, 우리가 수집한 사람의 수(방정식개수)가 변수의 개수 (키, 몸무게)보다 많을 때
dimension이 깊어질수록 앞 벡터와 뒤 벡터의 상수배 관계를 유지하기가 더 어려워지기때문이다.
'Basis > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 4. Singular Value Decomposition (1) | 2023.05.01 |
|---|---|
| [인공지능을 위한 선형대수학] 3.5 Eigendecomposition (0) | 2023.04.30 |
| [인공지능을 위한 선형대수] 2.1 Least Squares (1) | 2023.04.28 |
| Singular Value Decomposition (SVD) (0) | 2023.04.27 |
| [인공지능을 위한 선형대수] Onto / One-to-one func (0) | 2023.04.19 |




