Adore__
[인공지능을 위한 선형대수] 4. Singular Value Decomposition 본문
Source : [BoostCourse '인공지능을 위한 선형대수' - 주재걸 교수님]
eigendecomposition 와 비교해서 살펴보면 상당히 비슷한 점이 있다. 한번 비교해보자


- eigendecomposition은 Ax에서 A가 정사각행렬이었지만, SVD에서는 직사각행렬으로 허용범위가 넓어졌다.
- 또한 둘 다 A를 3개의 matrix로 분할하고, 조건이 있었다.
- eigendecomposition은 V가 가역행렬이고 D가 대각행렬이어야 한다.
- SVD는 U와 V transpose 는 각각 다 orthonormal matrix 이어야 한다. Sigma는 D와 마찬가지로 대각행렬이다.
- orthonormal 직교행렬 이란, 행렬의 모든 열벡터들이 길이가 1이고 서로 직교해야 한다.
- U의 column vector와 V의 row vector 모두 orthonormal이어야 한다. (V transpose가 orthonormal이어야 하므로 열벡터가 아닌 행벡터가 orthonormal)
그림으로 살펴보자

A가 위 그림과 같이 세로길이 m, 가로가 n 길이인 행렬일 떄, U는 mxm, V는 nxn 인 정사각행렬이다.
그리고 그 사이에 껴있는 sigma는 mxn 행렬이지만, nxn 크기만큼만 sigma 값으로 채워진 대각행렬을 가진다.
차원 축소 효과
위 그림의 곱 연산을 분석해보면,
행렬곱의 4가지 형태 중에서 가장 마지막 형태였던 sum of Rank 1 outer product로 해석할 수 있다.


위 그림처럼 U행렬은 (m개의 열 -> n개의 열) 로 줄어들고, Sigma 또한 mxn -> nxn 으로 차원이 줄어들어도
계산 결과는 같다.
즉, 차원 축소의 효과를 갖는다.
Another Perspective of SVD
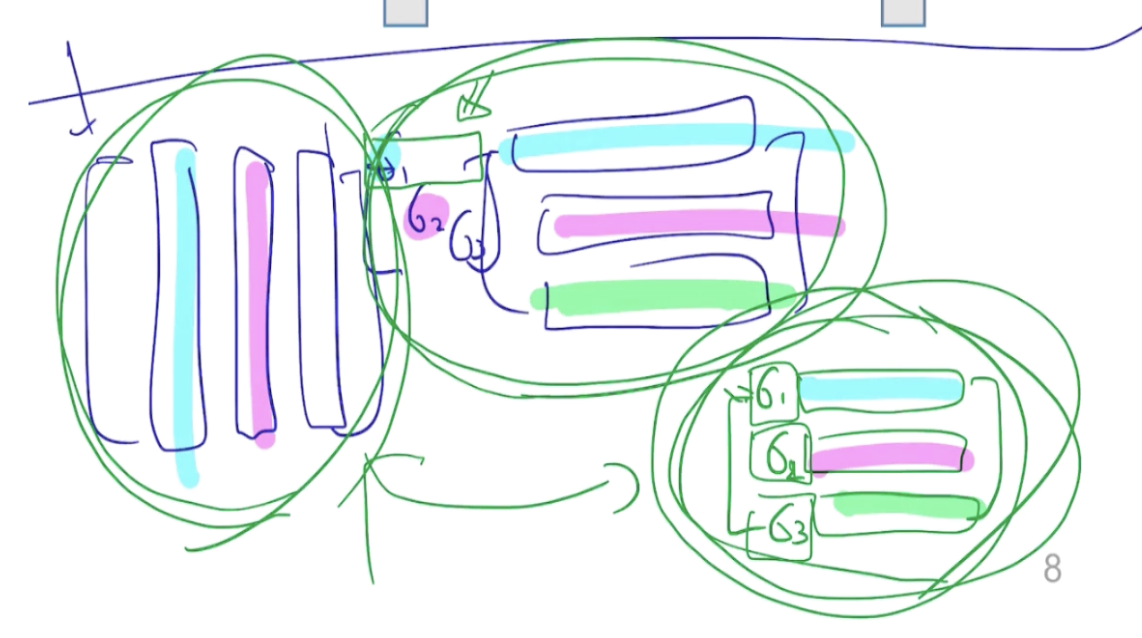
이를 약간 관점을 다르게 해서 봐보면, 행렬 A의 열벡터를 U의 열벡터에 선형 결합으로 표현하는 것이다.
이때 U는 orthonormal matrix이므로, 서로 선형독립이며 행렬 A를 span하므로 basis라고 할 수 있다.
마찬가지로 행렬 A를 transpose하면, 이번에는 U가 아닌 V의 열벡터가 A transpose의 열벡터의 basis가 된다.
(즉, V transpose의 행벡터가 A의 행벡터의 basis가 됨)

정리하면 U와 V transpose를
- A의 열공간의 orthonormal basis 집합인 U의 열벡터
- A의 행공간의 orthonormal basis 집합인 V transpose의 행벡터
이렇게 다시 설명할 수 있다. 이는 앞서 배웠던 그람슈미트 과정을 통해 (임의의 벡터 집합으로부터 직교집합 구하기) 구할 수 있다.
그런데 이러한 basis 집합은 유일할까?
그람슈미츠로 직교 벡터를 구할 때, 동일한 요소여도 순서를 바꾸면 다른 직교집합이 나온다.
따라서 유일하지 않다.
그렇다면 우리는 이러한 orthonormal basis 집합 U의 열벡터와 V transpose 행벡터를 따로따로가 아닌, 함께 연관지어서 찾아볼 수 있다. 이러한 관계를 보여주는 식은 바로 다음과 같다.

따라서 위 그림의 마지막 빨간 식을 만족하는 U와 V가 있을 때, 우리는 A를 SVD 할 수 있다.
Spectral Theorem
그러면 이 SVD를 어떻게 구하는가?
사실 SVD만을 위해 밝혀진 알고리즘은 없다. 결국 앞서 배웠던 eigendecomposition과의 유사성을 활용하여 SVD를 구하게 되는데,
이러한 연결고리가 어디서 존재하는지 찾아보자.
eigendecomposition의 수식형태과 유사하게 만들기 위해서 A에다가 A transpose를 곱한다.
우리의 아이디어는 AA(t)에 대한 eigendecomposition을 수행하여 얻어낸 U와 sigma 제곱, 그리고 U transpose가 실제로 eigendecomposition 했을 때의 V, D, V역행렬과 각각 같다진다는 것이다.
과연 이 가정이 맞는가?에 대한 답을 얻어보기 위해서는 다음과 같은 조건을 만족해야 한다.
▪️SVD의 조건

- 조건 1. AA(t)와 A(t)A를 각각 egendecomposition해서 뽑아낸 eigenvector들(U와 V의 열벡터들)이 다 수직인 (orthogonal) 관계를 만족해야 한다. (선형독립 관계만으로는 충분하지 않다. 서로 수직이어야 한다!)
- 조건 2. sigma 제곱은 diagonal matrix이며 각 eigen value들은 양수여야 한다.
- 기존 eigendecomposition을 보면, 가운데 diagonal metrix의 eigenvalue가 음수, 양수 모두 나올 수 있다.
- 그런데 sigma 제곱을 해버리면 이 eigenvalue를 복원하는 과정에서 허수가 나올 수 있다. 따라서 무조건 sigma 제곱은 양수여야 한다.
- (만약 AA(t)을 고유값 분해했는데, sigma 제곱의 원소에 -3이 나왔다고 하자. 우리는 여기서 singular vector인 A만 필요하기때문에 제곱근을 해버리면 -3의 루트, 즉 허수가 나오면서 실수 범위를 벗어나게 된다.)
기본적으로 분해를 하면, 무조건 n개의 orthonormal egen vector가 나오고, 이에 해당하는 eigen value들은 양수가 나오게 된다.
이를 U와 sigma square에 대입하면 조건이 맞아 떨어지게 된다.
- 조건 3. AA(t)를 eigendecomposition 해서 나온 eigen value(sigma square)와 A(t)A에서 나온 eigen value (sigma square)가 동일해야 한다.
▪️대칭행렬은 항상 대각화 가능
애초에 AA(t)와 A(t)A가 대각화가 가능한가?에 대한 근본적인 질문을 해보면, 항상 가능하다. 왜 그럴까?

A(t)A, AA(t) 이들은 기본적으로 symmetric (대칭)의 성질을 갖고 있다.
- '대칭 행렬'은 대각선을 기준으로 접었을 때 똑같은 값을 갖는다. 이 조건을 만족하려면, A = A(t)여야 한다.
- AA(t)의 transpose = AA(t) 이다. 즉, transpose해도 기존 행렬과 같으므로 symmetric하다.
이러한 symmetric matrix은 항상 대각화가 가능하다는 성질을 갖고 있다.
이때 주어지는 egen vector들은 서로 선형독립할뿐만 아니라 수직인 orthogonal한 성질을 갖고 있다
▪️대칭행렬의 Spectal Theorem
symmetric matrix의 또다른 성질을 보자 (spectral Theorem)

1) Symmetric matrix는 기본적으로 det를 취했을 때 허근이 나오지 않는다.
만약 허근이 나오면 n개의 linear independent 한 eigen vector를 뽑을 수 없다.
- 만약 5x5의 행렬 A가 있을 때, 고유값이 3, 5이고 lambda = 3일때 일중근, lambda = 5일때 이중근, 나머지 두개는 허근이라고 하자. 이때 얻을 수 있는 고유벡터는 고유값 3일때 1개, 고유값 5일때 2개가 나오고, 허근의 고유값일때는 고려하지 않는다.
- 따라서 5개의 고유벡터가 아닌 3개만 얻게 된다.
즉, 기본적으로 diagonalizable matrix의 필요조건은 고유값들이 중복을 허용해서 모두다 실근이 나와야한다는 것이다.
(5차방정식이면 5개 모두 실근이 나와야 한다)
2) 각각의 실근의 고유값에 해당하는 eigen space의 dimension (또는 basis의 개수)의 합은 기존 행렬의 차원의수 만큼 나와야한다.
- 5x5 행렬 A에 대한 고유값이 3과 2일 때, 3일때
- 고유공간의 차원 (고유벡터의 개수) + 5일때 고유공간의 차원 = 5 (행렬 A의 차원)
3) eigenspace끼리 수직이다. 즉, 서로 다른 고유값의 고유벡터들끼리 서로 수직이다.
- 고유값 3일때의 고유벡터와 고유값 5일때의 고유벡터는 서로 수직이다.
SVD 조건 1. 확인 : U와 V는 모두 orthogonal vector여야 한다!

대칭행렬의 고유값 분해 (= Spectral Decomposition) 를 했을 때 얻어지는 고유벡터 U는 orthonormal하므로 역행렬과 전치행렬이 같다. 따라서 UDU(-1) = UDU(t)라고 할 수 있다.
이 식을 풀어보면 크기가 1인 벡터들의 outer product 결과값을 각각 크기를 달리하여 (서로 다른 eigen value로 scaling) 더한 것과 같다.

SVD 조건 2. 확인 : sigma sqaure은 항상 양수가 나와야 한다!

positive definite 행렬의 특징을 살펴보자. 이는 우선 정사각행렬에서만 따질 수 있다.
x(t)Ax 곱셈을 하면 상수값이 나온다. 이는 양수일수도, 음수일 수도 있다. 하지만 어떤 특수한 행렬일 경우, 어떠한 x값을 넣어도 그 상수값이 항상 양수가 나온다. 이러한 행렬을 positive definite matrices라고 한다.
좀 더 쉽게 이해시키기 위해 이차방정식을 보자.
다음 함수는 x축 위에 떠있는 포물선이다. 즉, 어떤 x를 넣어도 y값이 항상 양수이다.

이처럼 f(x) = x(t)Ax 라고 할 때, 어떠한 x값에도 항상 양수가 나오는 정사각 행렬 A를 positive definite matrices라고 한다.
반면 결과 값이 0보다 같을 때도 있는 정사각행렬 A를 positive semi-definite 이라고 한다.

이런 positive definite인 경우에는 eigendecomposition 측면에서 고유값, 고유벡터들이 항상 양수가 나온다는 성질이 있다.
다만 어떤 positive definite 행렬에서는 n개의 선형독립인 eigen vector가 안나올 수 있다.
(5x5 행렬에서에서 3개의 고유벡터만 나올 수 있다. 실근이 3개밖에 안나오면 eigendecomposition이 불가능..하지만 어쨌건 찾을 수 있는 고유값에 대해서는 다 양수이다. 갯수는 부족할 지언정, 찾은 건 다 양수다!)
자, 이제 symmetric 하면서 positive definite한 행렬을 생각해보자.

symmetric 하므로 무조건 대각화가 가능하고, eigendecomposition이 가능하다.
다만 동시에 positive definite이므로, 모든 eigenvalues가 양수이다.
따라서 이러한 symmetric positive definite의 성질을 이용하려면 먼저 symmetric해야하고, positive definite 해아한다.
- AA(t)의 transpose = AA(t)이므로 symmetric하다.
-
- x(t)A(t) * Ax 로 나눠서 생각해보자
- [Ax]의 transpose * Ax이므로, 자기 자신의 내적과 같으므로 항상 양수가 나온다.A(t)A 는 positive definite 한가? x(t) A(t)A x 가 항상 양수가 나오는지 확인하자

따라서 조건 2. 항상 양수인 eigen value가 나오냐?를 만족할 수 있다.
조건 3. AA(t)와 A(t)A의 eigen value들이 서로 같은가?
이를 증명하는 것은 매우 간단한데, 생략하셨다.
🔻 정리
- SVD는 정사각행렬일 필요가 없고, 직사각행렬이어도 된다.
- AA(t)와 A(t)A공통적으로 나온 eigen value에 루트만 취하면, original A의 eigen value를 구하고 eigen vector를 구할 수 있다.
어떤 직사각행렬이 주어지던 간에, SVD는 항상 존재한다. (eigendecomposition은 존재할수도, 안할수도 있다.)
이를 정사각행렬에 적용하면 어떨까? 어떤 정사각행렬은 eigendecomposition이 없을 수 있지만, SVD는 항상 존재한다.
- eigendecomposition은 역행렬이 존재하고, linear independent한 V가 필요. 이러한 V를 이용하여 V inverse 행렬을 사용해야 함. 제한적.
- SVD는 orthonormal한 U가 필요하지만, V(t)는 U와 다른 벡터를 사용할 수 있음. 더 자유로움.
만약 들어온 matrix가 symmetric positive (semi-) definite이고 정사각행렬이라면,
eigendecomposition과 SVD 모두 항상 존재한다.
'Basis > Linear Algebra' 카테고리의 다른 글
| [인공지능을 위한 선형대수] 4.2 고유값 분해와 특이값 분해 응용 (0) | 2023.05.01 |
|---|---|
| [인공지능을 위한 선형대수학] 3.5 Eigendecomposition (0) | 2023.04.30 |
| [인공지능을 위한 선형대수] 2.2 Normal Equation (0) | 2023.04.28 |
| [인공지능을 위한 선형대수] 2.1 Least Squares (1) | 2023.04.28 |
| Singular Value Decomposition (SVD) (0) | 2023.04.27 |




